| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- FL
- control
- humble
- 제어공학
- Python
- 차량 동역학
- 2024적금
- RL
- #! /usr/bin/env python
- 자동제어
- ROS2
- 백스테핑
- 강화학습
- Backstepping
- ros2humble
- 나이퀴스트
- 비선형제어
- 나이퀴스트선도
- 터미널 오류
- 경로계획
- 우분투
- Isaac Sim
- 횡방향 동역학
- 오류
- 보드선도
- feedback linearization
- 러닝 #운동 #동기부여
- lateral dynamics
- 궤환선형화
- 궤환 선형화
- Today
- Total
내 머릿속
자동제어/제어공학 -5- 본문
이제 물리적인 모델들의 입력에 대한 출력인 전달함수로 나타내서 시뮬레이션을 돌려보았고
자동제어에서 해주어야할 일은 원하는 결과값이 나온 시스템이 아닌 그렇지 않은 시스템을
제어기를 설계해서 수정해 주어야 합니다. 제어기를 설계한다는 말은 전달함수를 조정해준다고 생각해도 되는데
전달함수를 지지고 볶는 과정에 대해 설명하겠습니다.
우선 어떤 유효한 방법에 따라 전달함수가 구해지고, 그 시스템 방정식이 연립 상미분방정식(ODE)일때 전달함수는 다항식의 비가 됩니다.
이 말은 즉슨
전달함수 G(s)가 (s^2+1)/s+1 같은 s에 관한 다항식의 분모 분자꼴로 나타난다는 말이고 여기서 새로운 개념이 하나 생깁니다.
극점, 영점
극점이란 전달함수를 무한대로 만드는 s값, 영점이란 전달함수를 0으로 만드는 s값입니다.

예를 들어 이런 전달함수가 존재한다면 극점과 영점은 각각 이렇게 구해집니다.
극점 : s = ±4i, -2/3
영점 : s = ±3i,-2/5
극점에 관한 자세한 내용은 나중에 설명하고 중요한건 극점이 +의 값을 가지면, s>0이 된다면 그 시스템은 불안정해집니다. 제어에서 제일 중요한건 안정된 시스템을 만드는 것이고 이는 극점이 모두 -값, s<0이 되어야 한다는 말입니다.
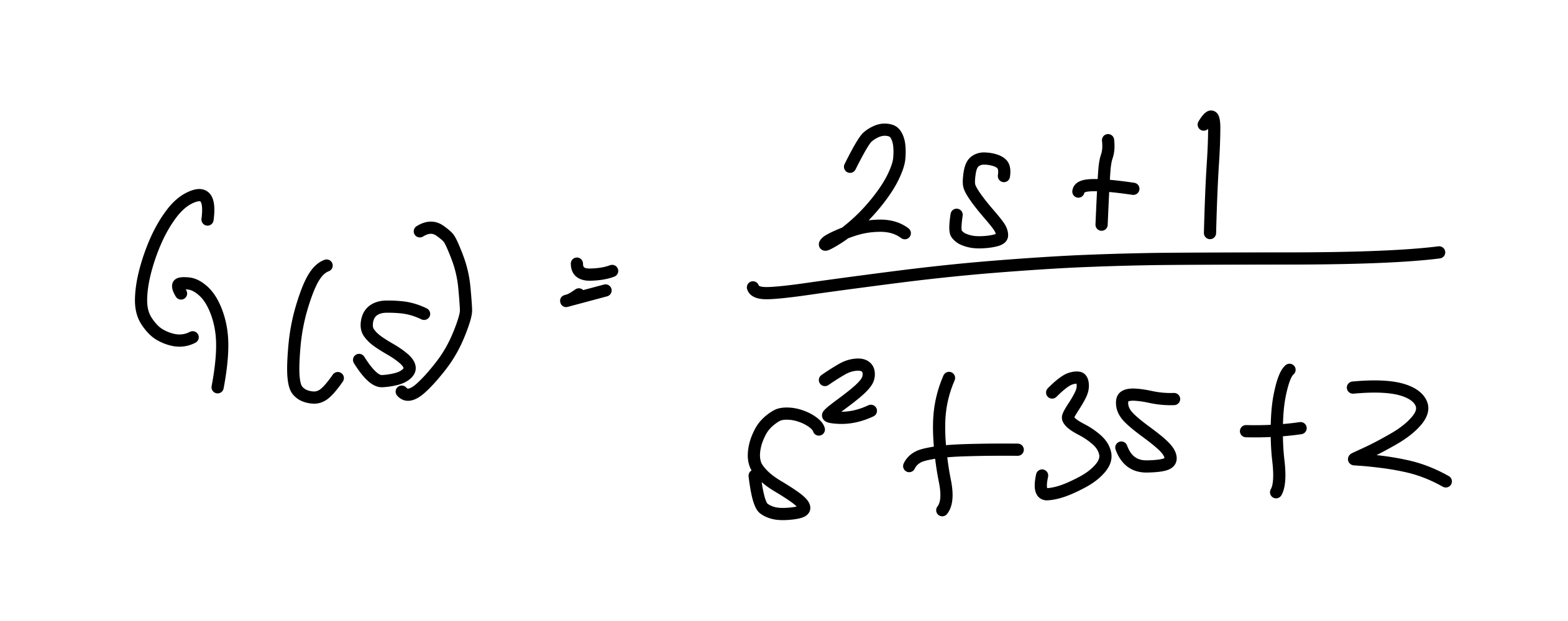
예를 하나더 들어보겠습니다.
이러한 입력과 출력간의 전달함수를 가지는 시스템이 있습니다.
그러면 극점은 s = -1, -2 영점은 s = -1/2가 됩니다.
극점이 음의 값을 가지기 때문에 시스템은 안정하다고 할수 있겠죠?

매트랩에서는 pzmap(num,den)를 쓰면 한번에 구할 수 있습니다.
보통 전달함수는 s-plane 허수 실수축에 나타냅니다. 이유는 x,y축은 허수를 표현할 수 없는데 전달함수의 극점과 영점이 허수를 포함하는 경우가 많기 때문입니다.
전달함수를 시간함수로 바꾸기 위해 부분분수 전개를하면

이렇게 되고 이를 라플라스 역변환을 통해

이와 같이 구할 수 있습니다. t가 무한대로 가면 e^-2t가 더 빨리 감쇠해 초반에는 3e^-2t가 시간응답의 초반부를 지배하지만 결국 -e^-t항은 나중에 주된 영향을 미치게 됩니다.
e^-2t에서 -2t에 해당하는건 전달함수의 극점이 결정하고 결국 시스템의 특성은 극점에 의해 결정된다고 할 수 있습니다.
'전공과목 정리 > 자동제어' 카테고리의 다른 글
| 자동제어/제어공학 (나이퀴스트 선도 그리기 2) (0) | 2022.09.30 |
|---|---|
| 자동제어/제어공학 (나이퀴스트 선도 그리기 1) (2) | 2022.09.30 |
| 자동제어/제어공학 -4- (매트랩 포함) (0) | 2022.07.18 |
| 자동제어/제어공학 -3- (0) | 2022.07.12 |
| 자동제어/제어공학 -2- (매트랩/시뮬링크 포함) (0) | 2022.07.02 |




