| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 차량 동역학
- humble
- 제어공학
- 자동제어
- Python
- 2024적금
- RL
- 경로계획
- 우분투
- 강화학습
- 보드선도
- 궤환선형화
- 백스테핑
- Backstepping
- 터미널 오류
- 나이퀴스트선도
- ROS2
- control
- lateral dynamics
- 오류
- 비선형제어
- #! /usr/bin/env python
- 나이퀴스트
- feedback linearization
- 러닝 #운동 #동기부여
- 궤환 선형화
- Isaac Sim
- FL
- ros2humble
- 횡방향 동역학
- Today
- Total
내 머릿속
자동제어/제어공학 -4- (매트랩 포함) 본문
저번 매트랩때는 인공위성의 회전운동 제어모델을 살펴봤는데 이번에는 진자운동을 모델링 해보겠습니다.

이러한 기본 진자운동 모델을 살펴보겠습니다.
O점(pivot)에 대해 운동방정식을 세워보면
m을 theta만큼 움직인 토크Tc가 존재하고, 회전운동이기 때문에
Tc - mg*g*l*sinθ = Iθ''
하지만 이 방정식은 sinθ가 존재해 비선형입니다. 지금은 비선형 방정식에 관해 다루진 않기 때문에 운동이 작다고 가정하고, sinθ = θ라고 가정함으로 선형화 시킬 수 있습니다.

결국 전달함수는 이와 같이 표현할 수 있습니다.
만약 m = 1kg / l = 1m / g = 9.81m/s^2 라고 가정한다면
분자는 1이 되고 분모는 s^2 + 9.81이 됩니다 이를 매트랩에서 실행해보면

이와 같은 시간응답이 나타납니다. 우리가 알고있는 공기저항이 존재하지 않을때 진자운동과 같은 형태를 보입니다.
그리고 저번 인공위성 모델에서 미소외란 토크 M_D가 존재하지 않는다면
입력Fc에 대한 자세θ의 전달함수는
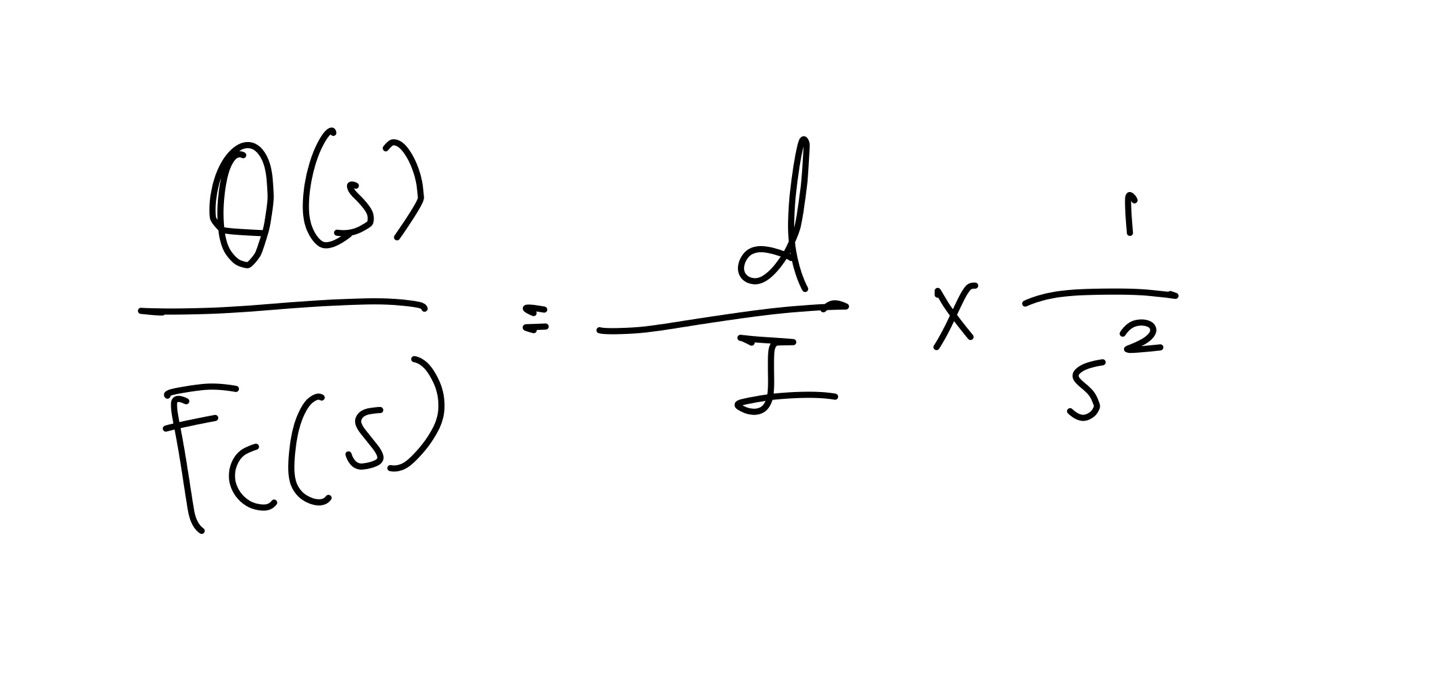
이렇게 도출가능하고 d가 1m이고, I가 5000kg-m^2라면
전달함수는 0.0002/s^2가 됩니다.
t=5sec에서 시작하는 0.1sec동안의 25N의 펄스에 대한 시스템 응답을 매트랩으로 구하면

대충 설명을 써두긴 했는데 이해안가시면 댓글 주세요.
그래프를 보면 첫번째 그래프에서 5초에 짧은 펄스입력이 들어갔고, 그 결과 비감쇠 시스템인 인공위성은 일정한 각속도로 밀리게 됩니다. 두번째 그래프가 이를 의미합니다.
'전공과목 정리 > 자동제어' 카테고리의 다른 글
| 자동제어/제어공학 (나이퀴스트 선도 그리기 1) (2) | 2022.09.30 |
|---|---|
| 자동제어/제어공학 -5- (0) | 2022.07.19 |
| 자동제어/제어공학 -3- (0) | 2022.07.12 |
| 자동제어/제어공학 -2- (매트랩/시뮬링크 포함) (0) | 2022.07.02 |
| 자동제어/제어공학 -1 (0) | 2022.06.30 |




